Pour résumer cet opérateur, nous allons présenter un cas assez
complexe extrait d'une analyse de <<En sourdine>>. Il s'agit donc d'un
cas d'isotaxémie, et l'isotopie visée est celle du sème /arbre/. Cette
isotopie ne contient pas de partie afférente, seule une partie
spécifique, dont les spécèmes sont :
('chênes', 'rossignol') ('chênes', 'gazon') ('arbousiers', 'gazon') et
('arbousiers', 'rossignol') pour le taxème //nature// et
('chênes noirs', 'désespoir') et ('chênes noirs', 'soir') pour le
taxème //mort//.
D'autre part, les deux taxèmes concernés ont leurs graphes
d'opposition représentés par les figures 
et
:
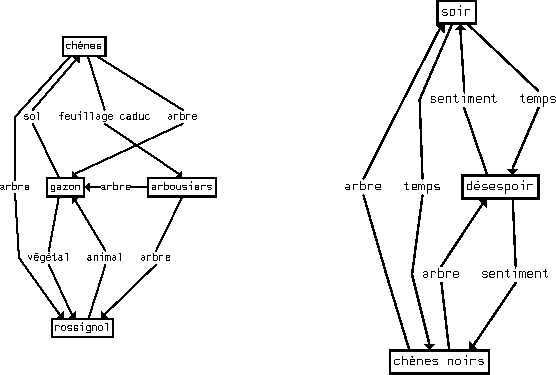
Figure: Taxème //mort// initial
Figure: Taxème //nature// initial
Après application de l'opérateur igen(/arbre/), diverses modifications ont eu lieu.
Tout d'abord, regardons le graphe d'opposition du nouveau
taxème
//arbre// ().
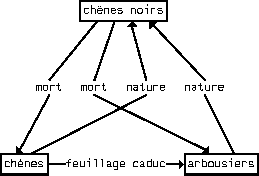
Figure: Nouveau taxème //arbre//
Comme il apparaît clairement dans cette figure, le sème spécifique
/feuillage caduc/ a été conservé entre 'chênes' et
'arbousiers' ; d'autre part les anciens sèmes microgénériques /nature/
et /mort/ ont maintenant des statuts spécifiques.
Regardons maintenant ce que les deux taxèmes initiaux sont devenus
( et ).
Figure: Nouveau taxème //mort//
Figure: Nouveau taxème //nature//
Dans ces taxèmes modifiés, les spécèmes initiaux ont été conservés. Cependant, nous pouvons remarquer que le sème /sol/, anciennement spécifique à 'gazon' n'apparaît plus dans le graphe de //nature//. Effectivement, la seconde projection du spécème qui le supportait a bien été supprimée du taxème : /sol/ est donc maintenant afférent à 'gazon'. Encore plus loin pour ce sème, puisqu'il n'est plus (pour l'ensemble de la structure) qu'afférent, cette opération va donc créer le nouveau taxème //sol// afin de satisfaire le problème de l'afférence pure. Ce taxème devra donc être rempli par deux nouveaux sémèmes (a priori non lexicalisés dans notre cas).
Enfin, aucune complétion des taxèmes précités n'est à effectuer, nous
pouvons en effet remarquer que les graphes correspondants sont
faiblement complets et que de chacun de leurs n 
uds est bien issu
au moins un arc.