Au sein d'un taxème donné, les spécèmes doivent couvrir un ensemble de
relations de distinction (d'opposition en fait). On obtient de cette
façon un graphe orienté dont les n 
uds sont les sémèmes d'un même
taxème. Ce graphe est complet, il y a pour chaque couple de sémèmes
s, s' d'un taxème t un spécème sp = (s,s') défini.
Par la suite, nous distinguerons les spécèmes activés, i.e. ceux qui supportent effectivement un sème, des spécèmes inertes, qui ne correspondent qu'à une caractérisation formelle. Ces derniers ne sont en fait que des sèmes spécifiques potentiels. Grâce à cette distinction, nous définissons ainsi un graphe partiel de spécèmes activés. Nous allons ici envisager les contraintes qui doivent organiser ce graphe partiel. Les spécèmes inertes seront en pointillés dans les différentes figures, alors que les spécèmes activés seront dessinés en continu.
Nous approfondirons l'exemple du taxème //couverts// pour exprimer les
contraintes s'appliquant aux spécèmes. Sans aucune activation, le
taxème est initialisé comme le montre la figure 
.
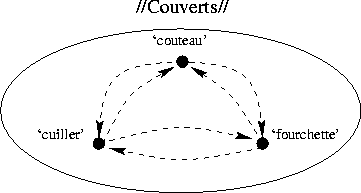
Figure: Activation du graphe d'opposition d'un taxème - première
étape
Considérons maintenant le spécème ('couteau', 'fourchette'), dans le
taxème //couverts// : si on lui attribue le sème /couper/ (nous
verrons comment plus loin), cela signifie simplement que le couteau
sert à couper, par opposition à la fourchette. Nous avons ainsi
une caractérisation positive de `couteau', mais pas de 'fourchette' ;
'couteau' possède donc un sème spécifique, mais pas 'fourchette'. Une
première conclusion est l'incompatibilité de cette attribution de sème
à celle qui correspondrait à attribuer le même sème /couper/ au
spécème ('fourchette', 'couteau') . La relation d'opposition entre les
deux sémèmes serait alors symétrique, et perdrait tout son sens. De la
même façon, on peut attribuer /couper/ à ('couteau', 'cuiller'),
c'est-à-dire rajouter un rôle distinctif au sème spécifique de
'couteau' ; mais 'couteau' ne reçoit pas pour autant de nouveau sème
spécifique. L'activation de ces deux spécèmes est représentée dans la
figure . Le problème à ce stade est l'absence de
caractérisation positive de 'cuiller' et 'fourchette'.
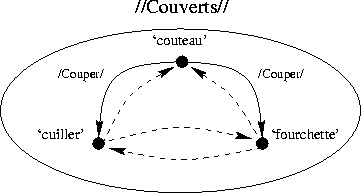
Figure: Activation du graphe d'opposition d'un taxème - deuxième
étape
Pour attribuer une caractérisation positive aux deux sémèmes 'cuiller'
et 'fourchette', nous pouvons activer les spécèmes
('cuiller', 'couteau') et ('fourchette', 'couteau') par le sème
/prendre/. Ces deux sémèmes ont donc un sémantème contenant chacun le
sème /prendre/, donc supportent bien une caractérisation positive. À
ce stade, représenté par la figure , nous avons bien la
présence pour chaque n ud d'un arc qui y prend son origine, donc une
caractérisation positive pour chaque sémème.
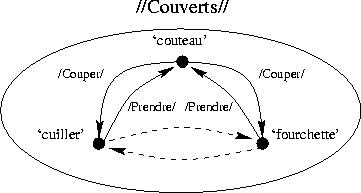
Figure: Activation du graphe d'opposition d'un taxème - troisième
étape
Mais 'fourchette' et 'cuiller' possèdent alors exactement les mêmes sèmes spécifiques. Du point de vue de leurs caractérisations sémantiques, la fourchette et la cuiller sont donc à ce stade indistinguables. Si l'on se contente pour palier à cette lacune de sur-activer le spécème ('fourchette', 'couteau'), par exemple en lui attribuant un autre sème comme /piquer/, nous distinguons alors les ensembles de sèmes spécifiques de 'fourchette' et 'cuiller'.
Un petit détour théorique s'impose alors. Rappelons que par les phénomènes et processus que nous décrivons, nous souhaitons, tout comme F. Rastier, proposer la description d'lune interprétation. Rappelons également qu'une interprétation n'est jamais véritablement achevée, et que la structure que nous décrivons actuellement ne capte qu'un minimum de stabilité nécessaire pour établir cette interprétation. Autrement dit, rien ne nous assure à ce stade de la description du taxème des couverts que le sème /piquer/ ne s'applique pas également au spécème ('cuiller', 'couteau').
C'est-à-dire que l'absence de détermination n'est pas une caractérisation.
La seule certitude que nous puissions avoir est que deux spécèmes opposés ne peuvent supporter le même sème. Par exemple, que l'on ne peut pas, sans bien sûr modifier la description déjà effectuée, attribuer /couper/ à ('cuiller', 'couteau').
Nous basant sur cette constatation, nous pouvons clairement voir le
seul moyen de distinguer avec certitude les deux sémèmes récalcitrants
: activer un des deux spécèmes qui les relient. C'est ce que nous
faisons en attribuant le sème /pour solides/ à ('fourchette',
'cuiller'), comme le montre la figure . La situation que
nous atteignons est donc une complétude non-orientée et la présence
d'un arc sortant pour chaque n ud.
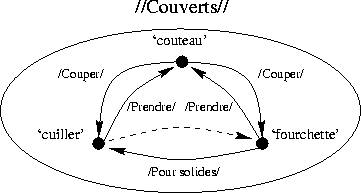
Figure: Activation du graphe d'opposition d'un taxème - dernière
étape