Définition :

Sème afférent : un sème se est afférent pour s si s est présent dans la troisième partie de l'isotopie de se. Soit : se est afférent pour s ssi .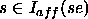

Nous ne distinguerons pas les sèmes spécifiques afférents des sèmes génériques afférents.