Sémèmes

C'est bien ici le problème le plus délicat, puisque nous avons déjà vu qu'il y a au moins deux manières de considérer la SE-identité des sémèmes.

Intéressons-nous pour l'instant à la SE-identité forte. Si et sont fortement SE-identiques, ils possèdent les mêmes sèmes, et ces sèmes ont pour eux les mêmes types. Par exemple, ils possèdent obligatoirement le même sème microgénérique, et le même sème mésogénérique si celui-ci existe. Ce sont donc, d'ores et déjà, deux sémèmes d'un même taxème. Donc, dans le graphe d'opposition de ce taxème, il existe un spécème activé, soit , soit , soit les deux. Considérons que ce soit , et qu'il lui soit attribué le sème se. Ce sème se est donc spécifique pour . Il doit également être spécifique pour (hypothèse de travail). Donc, il doit exister un spécème dans . ne peut être identique à (principe d'opposition), donc nous avons déjà la contrainte que le taxème de doit contenir au moins trois éléments. 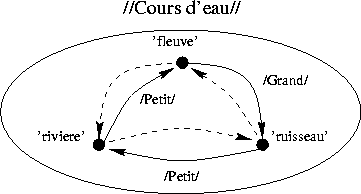Il apparaît donc que le cas où la S-identité forte n'est pas établie entre et est celui d'un cycle formé par les spécèmes de l'isotopie spécifique étudiée. Par exemple, au sein du taxème des //cours d'eau//, les sémèmes 'ruisseau', 'rivière', 'fleuve', peuvent s'articuler de façon minimale comme indiqué par la figure .

  
Figure: Exemple de cycle

Dans ce cas, les deux sémèmes 'ruisseau' et 'rivière supportent le même sème spécifique /petit/ : leurs sémantèmes sont identiques, même si les contraintes précisées pour les isotopies spécifiques sont respectées dans ce taxème. En fait, la véritable identité sémantique d'un sémème, centrée sur ses sèmes spécifiques, prend en compte non seulement le sème, mais aussi le sémème auquel ce sème sert à opposer le premier. C'est cette idée d'identité structurelle qui nous a conduit à préciser les contraintes (en fait à les limiter). Ainsi, considérer la simple collection de sèmes spécifiques attribués à un sémème, sans considérer la seconde projection des spécèmes correspondants, ne permet par la distinction de deux sémèmes d'un même taxème.

Cette vision d'un sémème comme ensemble de sèmes, même typés, n'est en fait qu'une projection de la structure sémantique complète à des fins calculatoires et/ou typologiques comme nous le verrons par la suite. La véritable forme de l'identité sémantique serait donc la suivante :

La fonction id permet donc de résumer toutes les considérations sémiques précisément typées attribuées à un sémème, avec les spécifications suivantes :

• est le sème microgénérique du sémème.
• est le sème mésogénérique du sémème, s'il existe.
• La famille des , avec et rappelle les sèmes spécifiques du sémème s, en précisant les sémèmes de son taxème qui s'opposent à lui par le sème . En fait, ces couples traduisent l'existence d'un spécème dans l'isotopie du sème .
• Enfin, les sont les sèmes afférents du sémème s.

• Théorème :
• Démonstration :