Maintenant que nous avons circonscrit la zone de localité sémantique qu'est le taxème, dans le but de traduire les différences de signifiés en oppositions, précisons la nature de ces relations spécifiques. Cette étape, se situant pleinement dans ce que nous avons identifié comme la couche logique de notre application, doit rejeter toute imprécision dans son développement. La simplicité générale de cette dernière doit être équilibrée par une grande rigueur formelle, et nous verrons que la notion de sème spécifique et celle d'opposition qu'elle véhicule est centrale.
Si nous reprenons l'exemple obsessionnel du taxème //couverts//, contenant `fourchette', `couteau' et autre `cuiller', il va nous falloir exprimer via des sèmes les oppositions entre ces unités.
Or, on trouve ([24] p. 52) : << ... la relation entre deux sèmes spécifiques << permettant d'opposer deux sémèmes voisins >> est une relation d'incompatibilité ; elle induit entre les sémèmes qui les incluent une relation de disjonction exclusive >>.
L'opposition (entre les sémèmes) est donc bien cette relation de
disjonction exclusive dont parle la sémantique interprétative. Par
contre, la notion d'incompatibilité doit être étudiée plus
attentivement. En logique, l'incompatibilité est une relation très
forte, exprimée par le fait que deux entités incompatibles ne peuvent
jamais coexister dans une entité supérieure. Prenons
l'exemple que donne F. Rastier pour les couverts : il attribue /pour
prendre/ à fourchette et /pour couper/ à couteau, et se base sur
l'incompatibilité de ces deux sèmes (donc a priori une relation
absolue entre entités d'un niveau d'abstraction élevé) pour induire
l'opposition entre ces deux sémèmes. Le schéma 
illustre
cet état de fait.
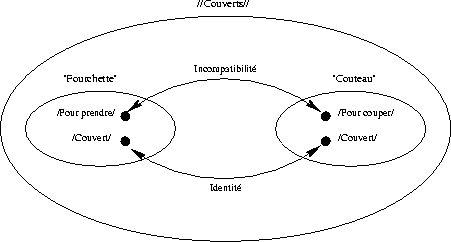
Figure: Incompatibilité des sèmes spécifiques et opposition des
sémèmes
Considérer l'incompatibilité dans un sens logiquement fort implique donc que l'on ne peut trouver aucun sémème auquel soient attribués ces deux sèmes. Cela suppose également que la langue nous fournit un réseau complet de sèmes incompatibles, comme les éléments de définition d'un système logique. Ou bien la notion d'incompatibilité logique est trop forte, et nous pouvons nous contenter de relations locales (par exemple limitées à la zone du taxème), auquel cas ce terme d'incompatibilité devrait être évité.
Un autre point intéressant est le suivant : un seul sème spécifique défini de la façon précédente ne peut suffire à exprimer une relation binaire entre sémèmes : l'incompatibilité doit être établie entre deux sèmes pour induire l'opposition entre sémèmes. Par conséquent, la notion de taxème à un seul élément est inintelligible.
Toutes ces considérations vont donc nous conduire à remanier quelque peu la <<forme>> des sèmes spécifiques, avec en tête les objectifs suivants :